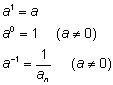|
|
||||||||||||||||
|
|||||||||||||||||
Diese Seite gehört zu einem Artikel von Manfred Scholz zur Reifenbeschriftung. Mathematik am ReifenDer Load Index lässt sich auch berechnen. Als Beispiel soll uns hier die folgende Reifenbezeichnung dienen: von: 195/65 R 15 91 H zu: MAX LOAD 615 KGS (1355 LBS) Die Umrechnung von nichtmetrischen Einheiten in die metrischen Einheiten stellt kein wesentliches Problem dar, wenn bekannt ist, wie breit ein Männerdaumen sein sollte. Ganz anders die mathematische Leistung, wenn die Tragfähigkeit eines Fahrzeugreifens aus einem Index –einem nichtssagendem Symbol ermittelt werden soll. Mit der geheimnisvollen Formel
lässt sich die Tragfähigkeit Tkg durchaus brauchbar in kg berechnen. Dazu ist nur der Rückblick auf Potenzen notwendig. PotenzenNach Addition/Subtraktion und Multiplikation/Division sind die Rechenoperationen der dritten Stufe das:
Ein Produkt aus n gleichen Faktoren heißt Potenz:
a · a · a · ... · a = a n
n Faktoren Nach dieser Festlegung darf n nur eine natürliche Zahl außer 0 und 1 sein, da ein Produkt mindestens zwei Faktoren besitzen muss. Dieser Potenzbegriff wird erweitert durch die Definitionen
Damit ist an für alle ganzzahligen Exponenten definiert, allerdings für n ≤ 0 mit der Einschränkung a allgemein: an = b a = Basis
n = Exponent
b = Potenzwert Beispiel: 53 = 125 102 = 10 · 10 = 100 103
= 10·
10
·
10 = 1 000 106
= 10·
10
·
10 ·
10
·
10 ·
10= 1 000 000 Bei einem Tragfähigkeitsindex von 91 würde sich eine Potenz von 1091 ergeben – also eine Eins mit 91 Nullen. Der Taschenrechner oder der PC kann diese wissenschaftliche Schreibweise meist nur einzeilig darstellen. Dann ergibt sich eine Anzeige „1 E+91“ für den Exponenten 91 zur Basis 10.
Radizieren (Wurzelziehen) Basis a und Exponent n einer Potenz sind für a ≠ 0 im allgemeinen nicht vertauschbar: an ≠ na. Deshalb hat das Potenzieren zwei Umkehroperationen. Mit der einen, dem Radizieren, lässt sich bei gegebenem Potenzwert und Exponenten die Basis berechnen. Ist b einen nichtnegative reelle Zahl und n eine natürliche Zahl außer Null, so heißt die eindeutig bestimmte nichtnegative reelle Zahl a, deren n-te Potenz b ist, die n-te Wurzel aus b:
Die dritte Wurzel wird auch Kubikwurzel genannt. Die Potenz einer positiven reellen Zahl a mit einem rationalen Exponenten
ür m = 1 gilt: Beispiele:
Jede Rechnung mit einer Wurzel lässt sich auch als Rechnung mit Potenzen durchführen. Aus
der Tragfähigkeitsformel wird
Für
den TI von 91 ergibt sich
Tkg
= 617 kg Damit kommt der Rechenwert dem abgelesenen Tabellenwert von
615 kg sehr nahe und ist ausreichend genau.
Aufgabe
1.
Erstellen Sie nach der Formel
die einzelnen Tragfähigkeitswerte
2.
Erstellen Sie das dazugehörige Diagramm
Lösung Die Berechnung erfolgte mit dem Kalkulationsprogramm MS-EXCEL. Als Formel wurden zur Eingabe folgende Befehle benutzt: = 45*POTENZ(10;A3/80) Die Basis ist 10. In der Zelle A3 steht der entsprechende Load Index (hier 50), der Exponent ist gebrochen rational 50/80. Diese Seite von kfztech.de weiter empfehlen Johannes Wiesinger bearbeitet: Folgen Sie kfztech auf Twitter Besuchen Sie kfztech auf Facebook Lesen Sie auch den Blog von kfztech.de |
|
||||||||||||||||
|
|||||||||||||||||